leetcode hot 100 题解

leetcode hot 100 题解

1. 深度搜索（recursive 解法）

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

<
1
2
输入：nums = [0]
输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10
  • nums 中的所有元素 互不相同

题解：

img

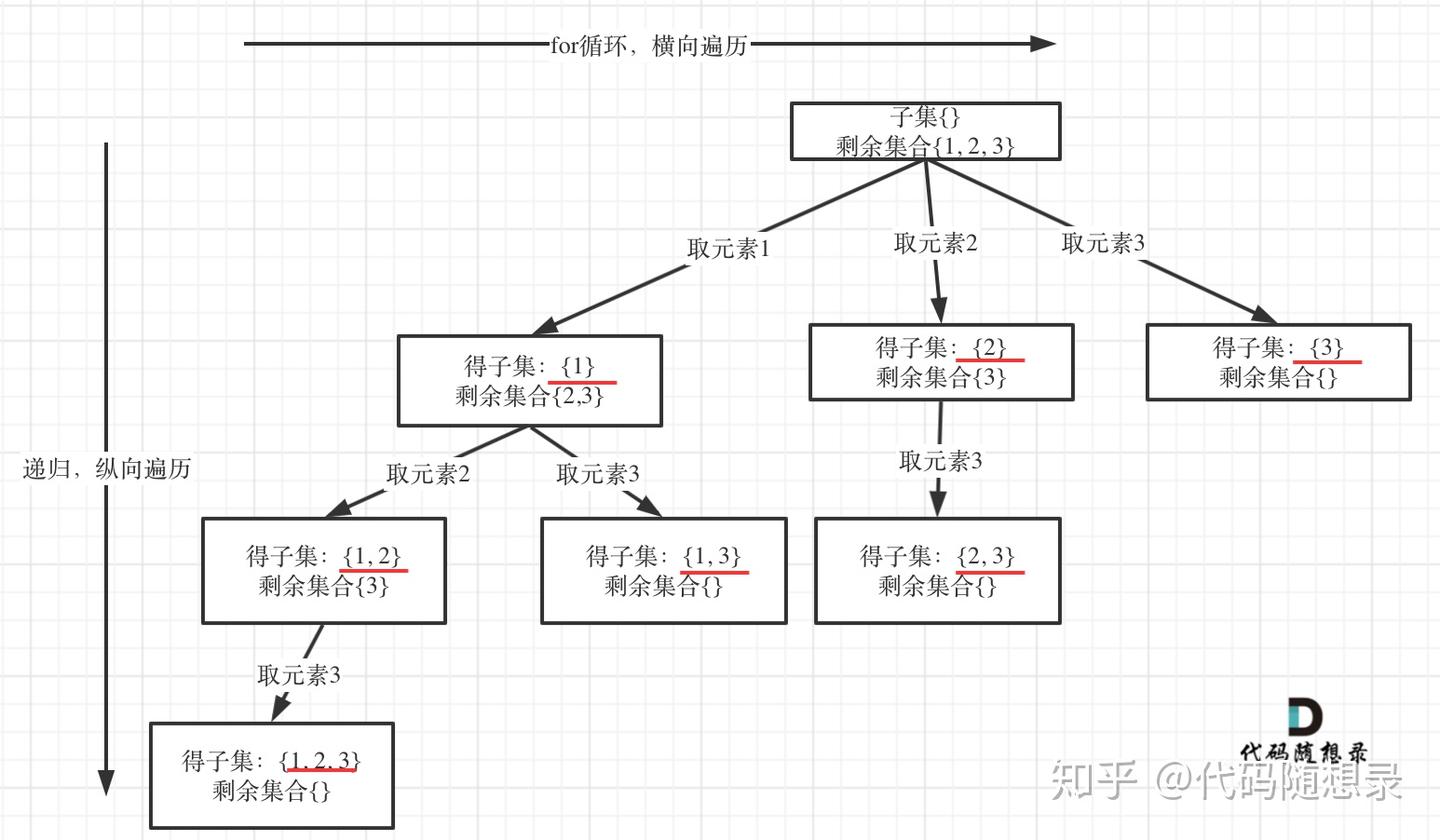
调用：dfs(0, [])

  • 得子集：{}
  • 剩余集合：{1,2,3}
  1. 第一层 for 循环
  • i=0 → 取元素 1 → path=[1]，进入 dfs(1,[1])
    • 得子集：{1}
    • 剩余集合：{2,3}
  • i=1 → 取元素 2 → path=[2]，进入 dfs(2,[2])
    • 得子集：{2}
    • 剩余集合：{3}
  • i=2 → 取元素 3 → path=[3]，进入 dfs(3,[3])
    • 得子集：{3}
    • 剩余集合：{}

深入第一条分支（i=0，选了 1）

  • 在 dfs(1, [1]) 里：
    • for 循环 i=1：取 2 → path=[1,2] → dfs(2,[1,2])
      • 得子集：{1,2}
      • 剩余集合：{3}
      • 再往下，取 3 → path=[1,2,3] → dfs(3,[1,2,3])
        • 得子集：{1,2,3}
        • 剩余集合：{} （递归结束）
      • 回溯 pop 掉 3 → 回到 {1,2}
    • for 循环 i=2：取 3 → path=[1,3] → dfs(3,[1,3])
      • 得子集：{1,3}
      • 剩余集合：{}

下面是回朔具体流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
ENTER dfs(start=0, path=[]) | remaining=[1, 2, 3]

snapshot added -> res=[[]]

choose nums[0]=1

after append -> path=[1]

ENTER dfs(start=1, path=[1]) | remaining=[2, 3]

snapshot added -> res=[[], [1]]

choose nums[1]=2

after append -> path=[1, 2]

ENTER dfs(start=2, path=[1, 2]) | remaining=[3]

snapshot added -> res=[[], [1], [1, 2]]

choose nums[2]=3

after append -> path=[1, 2, 3]

ENTER dfs(start=3, path=[1, 2, 3]) | remaining=[]

snapshot added -> res=[[], [1], [1, 2], [1, 2, 3]]

EXIT dfs(start=3)

backtrack pop 3 -> path=[1, 2]

EXIT dfs(start=2)

backtrack pop 2 -> path=[1]

choose nums[2]=3

after append -> path=[1, 3]

ENTER dfs(start=3, path=[1, 3]) | remaining=[]

snapshot added -> res=[[], [1], [1, 2], [1, 2, 3], [1, 3]]

EXIT dfs(start=3)

backtrack pop 3 -> path=[1]

EXIT dfs(start=1)

backtrack pop 1 -> path=[]

choose nums[1]=2

after append -> path=[2]

ENTER dfs(start=2, path=[2]) | remaining=[3]

snapshot added -> res=[[], [1], [1, 2], [1, 2, 3], [1, 3], [2]]

choose nums[2]=3

after append -> path=[2, 3]

ENTER dfs(start=3, path=[2, 3]) | remaining=[]

snapshot added -> res=[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3]]

EXIT dfs(start=3)

backtrack pop 3 -> path=[2]

EXIT dfs(start=2)

backtrack pop 2 -> path=[]

choose nums[2]=3

after append -> path=[3]

ENTER dfs(start=3, path=[3]) | remaining=[]

snapshot added -> res=[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]

EXIT dfs(start=3)

backtrack pop 3 -> path=[]

EXIT dfs(start=0)



FINAL res = [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]

Python 答案 

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        def dfs(start,path):
            res.append(path[:])
            for i in range(start,len(nums)):
                path.append(nums[i])
                dfs(i+1,path)
                path.pop()
        dfs(0,[])
        return res

2. 快速选择

215. 数组中的第K个最大元素

**题目：**给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 :

输入: [3,2,1,5,6,4] 和 k = 2

输出: 5

先学一下什么是快速排序(Quicksort)

快速排序的思想其实很简单，就 3 步：

  1. 挑一个基准数 (pivot)

    • 随便选一个，比如数组第一个或最后一个。

  2. 分区 (partition)

    • 把比 pivot 小的放一边，比 pivot 大的放另一边。
    • pivot 最后就“放到正确的位置上”。

  3. 递归左右两边

    • 左边继续排，右边继续排。

举个例子：排 [3, 2, 1, 5, 6, 4]

  1. pivot=3
    • 比 3 小的：[2,1]
    • 比 3 大的：[5,6,4]
    • 得到 [2,1] + [3] + [5,6,4]
  2. 排 [2,1] → 得 [1,2]
  3. 排 [5,6,4] → 得 [4,5,6]

拼起来 → [1,2,3,4,5,6]

快速选择 (Quickselect)

问题：如果我们只想要「第 k 大元素」，还需要整个数组都排好吗？

👉 不需要！

快速选择就是：

  1. 用快速排序的分区方法，确定 pivot 的位置。
  2. 看 pivot 的位置和 k 的关系：
    • 如果正好等于 k → 找到了！
    • 如果 k 在左边 → 只递归左边。
    • 如果 k 在右边 → 只递归右边。

这样就比快排快，因为它只递归 一边。

🌰 举个例子：找 [3, 2, 1, 5, 6, 4] 里的第 2 大

数组 [3,2,1,5,6,4]，k=2（第二大的数是 5）。

  1. pivot=3 → partition → [5,6,4,3,2,1]

    • pivot 的位置是 3（第 4 大）。
    • k=2 在左边，所以只递归 [5,6,4]。

  2. 子数组 [5,6,4]，pivot=5 → partition → [6,5,4]

    • pivot 的位置是 1（第 2 大）。
    • ✅ 找到了！结果是 5。

时间复杂度

  • 每次 partition O(n)
  • 但每次只递归一边（大约一半大小）
  • 平均复杂度 O(n)

让我们回到这个题 ， 根据上面讲的内容，我们需要完成两个函数 ， partition 和 select 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def partition(left, right, pivot_index):
        """对区间 [left, right] 做分区，返回 pivot 的最终位置"""
        pivot = nums[pivot_index] # 设置基准数

        # 1) 把 pivot 先移到末尾，腾出位置
        nums[pivot_index], nums[right] = nums[right], nums[pivot_index]

        # 2) store_index 指向“左区间”的尾部；左区间里放的都是 > pivot 的
        store_index = left
        for i in range(left, right):
            if nums[i] > pivot:                 # 注意这里用 '>'，因为我们要“第 k 大”
                nums[store_index], nums[i] = nums[i], nums[store_index]
                store_index += 1

        # 3) 把 pivot 放回“中间”，它左边全都 > pivot，右边全都 <= pivot
        nums[store_index], nums[right] = nums[right], nums[store_index]
        return store_index  # 这个位置就是 pivot 的“从大到小”的最终排名（0-based）

我们在 partition（分区） 时，需要：

  1. 遍历 [left, right-1]，把比 pivot 大的数放到前面。
  2. 遍历过程中，pivot 不能“碍事”。
  3. 所以先把 pivot 暂时放到末尾，最后再把它放回正确位置。

store_index 指针指向最左边 left ，然后从左往右遍历把比 pivot大的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def select(left, right, idx):
        """在 [left, right] 内找到“从大到小第 idx (0-based) 的元素”"""
        while True:
            if left == right:
                return nums[left]

            # 随机化 pivot，降低退化到 O(n^2) 的概率
            pivot_index = random.randint(left, right)
            pivot_index = partition(left, right, pivot_index)

            if idx == pivot_index:
                return nums[pivot_index]
            elif idx < pivot_index:
                right = pivot_index - 1   # 目标在“更大”的左半边
            else:
                left = pivot_index + 1    # 目标在“更小”的右半边

    return select(0, len(nums) - 1, target)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import random
from typing import List

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        target = k - 1  # 从大到小第k大 -> 0-based

        # 三路分区：把区间 [left, right] 按 pivot 值分成三段
        # 结束后满足：
        #   nums[left:lt]     > pivot
        #   nums[lt:gt+1]    == pivot
        #   nums[gt+1:right+1] < pivot
        # 返回 (lt, gt) —— 等于 pivot 的闭区间
        def partition(left: int, right: int, pivot_index: int):
            pivot = nums[pivot_index]
            nums[pivot_index], nums[right] = nums[right], nums[pivot_index]  # 先把 pivot 挪到末尾，便于操作
            lt, i, gt = left, left, right
            while i <= gt:
                if nums[i] > pivot:                 # 放入“更大”区
                    nums[lt], nums[i] = nums[i], nums[lt]
                    lt += 1
                    i += 1
                elif nums[i] < pivot:               # 放入“更小”区
                    nums[gt], nums[i] = nums[i], nums[gt]
                    gt -= 1                         # i 不动，检查换过来的元素
                else:                                # 等于 pivot
                    i += 1
            return lt, gt

        left, right = 0, len(nums) - 1
        while True:
            if left == right:
                return nums[left]
            pivot_index = random.randint(left, right)
            lt, gt = partition(left, right, pivot_index)

            if target < lt:            # 目标在“更大”的左段
                right = lt - 1
            elif target > gt:          # 目标在“更小”的右段
                left = gt + 1
            else:                      # 命中等于段
                return nums[target]
笔记
#笔记 #leetcode #算法
leetcode hot 100 题解
http://example.com/2025/09/23/leetcode hot 100 题解 /
Author
John Doe
Posted on
September 23, 2025
Licensed under