大模型算法学习笔记（1） - PPO 算法

1. 前置概念

PPO 算法 最开始用在 强化学习 中

强化学习思想：在环境中试错并获得奖励（正或负），然后将其视作反馈从而学习

其中，负责决策和试错的智能体我们成为 agent ，可以简单的类比成监督学习中的机器学习或深度学习模型 ，是一个可学习的函数 。

我们将传统强化学习的过程应用在大模型中：

episode ：语言模型生成一个句子

step：句子中的每一个 token

在第 t 个 step 时 ，agent 和环境交互包含以下步骤：

1. agent 收到来自环境的状态 $S_t$
2. 基于该状态$S_t$ ，agent采取的动作 $A_t$
3. 环境进入新状态 $S_{t+1}$
4. 环境给 agent 带来一些奖励 $R_t$

上面这个整个步骤 在大模型中 就是：

agent（模型） 当前的状态 $S_t$（当前已经生成的句子） ,采取的动作（生成一个token）$A_t$ 然后进入下一个状态$S_{t+1}$，然后环境（打分函数或者模型）基于当前的agent 去给agent 一个 $R_t$ 也就是loss之类的 ，我们希望在大模型每次做action（query）的时候 ，采取的是概率最大的那个 token 。我们希望最后的 Reward 也是最大的。

2. Actor-Critic 算法

Actor : agent ，做决策的模型

Actor 会在 当前状态 $S_t$ 选择 action ， 这里就有一个概率分布 P($A_t$|$S_t$) (LLM中最后的Softmax)

Critic : 辅助模型负责预测动作的收益，预测选择 $A_t$之后到结束为止的奖励之和的期望$Q(S_t,A_T)$(状态动作价值)，在LLM中就是第二个模型

实际训练中需要 ：基准模型 ，训练模型 ，奖励模型 ，状态价值模型

基准模型：冻结不动的 （HSVS）

训练模型（Actor）：训练的模型 （HSVS）（Lora或者FFT）

奖励模型：LLM预训练，最后一层换成 Linear Head （HS1）

状态价值模型（Critic）：LLM 挂一个Value Head ，冻结参数，（HS1）

然后我们在回到 AC 算法 ，我们这里就很好立即这里的 Actor 和 Critic 了 ，Actor 就是要训练的模型，模型输入的向量是 $S_t$ , 概率分布 $P(A_t|S_t)$ 就是生成下个token的概率分布, Critic 就是这里的 “ LLM 挂一个Value Head” ，负责预测状态动作价值，如下图所示 Reward 模型就是这里的Critic ，输入当前的 token 预测未来的reward也就是这里的$Q(S_t,A_T)$

那么就好办了 ，我们的 Loss 就可以计算出来：

$loss = -log[ P(A_t|S_t)]Q(S_t,A_t)$ ,然后就可以用 loss去更新模型参数（梯度下降），这里的loss就是大模型的Loss

这里可以理解成当前状态下的概率分布 * 当前的期望 Reward （这里用策略梯度公式推出来的特别复杂，不展开）

我们回到前面的强化学习流程，可以写成 ：

在第 t 个 step 时 ，agent 和环境交互包含以下步骤：

1. agent 收到来自环境的状态 $S_t$
2. 基于该状态$S_t$ ，agent采取的动作 $A_t$，critic 计算出未来的reward期望 $Q(S_t,A_t)$（包括当前） , 然后演员可以用 $loss = -log P(A_t|S_t)Q(S_t,A_t)$ 更新参数
3. 环境收到$A_t$ 进入新状态 $S_{t+1}$, 更新参数的演员生成 $A_{t+1}$
4. 环境给 agent 带来一些奖励 $R_t$, critic 用 $loss = [Q(S_{t+1},A_{t+1}) + R_t - Q(S_t,A_t)]^2 $

对演员来说：

• 如果 $\hat{A}t>0$，说明该动作比平均水平好，损失项会是正数；梯度 会推动模型增大该动作的概率。优势越大，梯度的幅度越大，更新力度越大。
• 如果 $\hat{A}_t<0$，则说明这个动作表现差，损失项为负，梯度方向相反，促使模型降低该动作的概率；绝对值越大，惩罚力度越大。

对评论家来说：

• 如果 Critic 低估了价值（预测 < 真实目标），loss 会变大，梯度推动 Critic 把预测抬高。
• 如果 Critic 高估了价值（预测 > 真实目标），loss 也会变大，梯度推动 Critic 把预测压低。

3. Advantage Actor-Critic（A2C）算法

A2C 算法是 Actor-Critic 算法的改良

1. 演员收到环境的状态 $S_t$ ,生成动作 $A_t$
2. 环境收到 $A_t$ 之后给出奖励 $R_t$ , 和新状态 $S_{t+1}$
3. 评论家估计状态价值 $V(S_t)$ ,$V(S_{t+1})$ 并计算优势 Advantage ，$Adv(S_t,A_t) = V(S_{t+1}) + R_t - V({S_t})$

​ (这个其实就是前面Critic 的loss)

4. 演员用 $ loss = - log{p(A_t|S_t)Adv(S_t,A_t)}$ 更新参数
5. 评论家用 $loss= [Adv(S_t,A_t)]^2$（和之前保持一样） 更新参数

4. PPO 算法

PPO算法就是在 A2C算法的基础上更改了 演员的$loss$ 为 $loss = -\frac {p(A_t|S_t)}{p’(A_t|S_t)}Adv(S_t,A_t)$

${p’(A_t|S_t)}$ 是 old policy ， 上面是 new policy

其中p是本次参数更新前的策略，p’是上一次参数更新前的策略（梯度是不会回传到p’的），这个p’就是我们找来限制p的东西。

熔断机制

为了方便描述，我们令 $r(A_t,S_t)=\frac {p(A_t|S_t)}{p’(A_t|S_t)}$

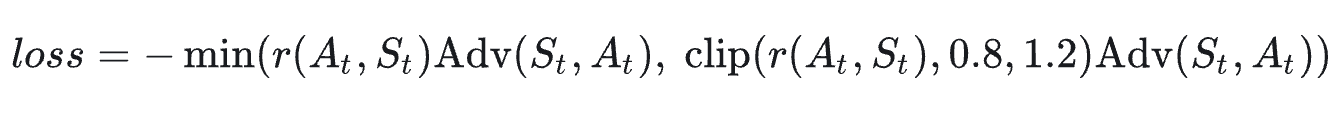
其中clip(r, 0.8, 1.2)表示：当r小于0.8时，clip函数值为0.8，当r大于1.2时，clip函数值为1.2，否则clip函数值为r。来验证一下新的loss是否实现了“熔断机制”吧：

• Adv大于0：r大于1.2之后，min操作就会取右边的值；此时loss中就只剩常量了，不产生任何梯度；而r无论多小都还是会产生梯度
• Adv小于0：r小于0.8之后，min操作就会取右边的值，此时loss中就只剩常量了，不产生任何梯度；而r无论多大都还是会产生梯度

我们用一句简单的话来总结PPO算法：

根据优势决定是否强化动作的，限制更新幅度的，带有熔断机制的强化学习优化算法

5.Policy Gradient

传统的 gradient 是 descent $\theta$ -> $\theta$ - LR * gradient , gradient 通过 loss 计算 ，

policy gradient 是 descent $\theta$ -> $\theta$ + LR * gradient * reward